Astronomy of Greece Print

Astronomy of Greece

Note: Remember you are responsible for graphs, charts and other items that form part of the overall summary of this topic.

I) The Astronomy of Ancient Greece

A) Based on the astronomy of Babylon and Egypt

1) Heavily influenced by astrology

B) Astrology is not the same as astronomy

1) Not a science

2) Belief that heavenly bodies influence and control human lives and feelings

C) Astronomy is a science

1) Study of celestial bodies

(a) Magnitude

(b) Motions

II) Important figures

A) Thales (624-546 BCE)

1) Founder of Greek astronomy

2) Founder of the Milesian (pre-Ionian) School

3) Predicted an eclipse (about 585 BCE)

(a) Halted a war between the Medes and the Lydian’s

(b) Thales’ action revealed the great strengths of astronomers at this time

(1) These events had a disturbing effect on public behavior

(2) Astronomers became important to rulers

4) Little else is known of Thales

(a) Unknown whether he believed if the Earth was flat or spherical

(b) Genius lay in his emphasis on gaining knowledge through observation of natural phenomena

(d) Began the search for the natural causes of celestial phenomena

B) Anaximander (610-546 BCE)

1) Believed the Universe was contained within the rim of a huge wheel filled with fire

(a) The holes in the rim, through which the fire could be seen, were the planets and the stars

2) First philosopher who speculated that the sky contained separate spheres through which the planets traveled

(a) Concept dominated astronomical thought up to the 17th century

3) Explained the existence of the ‘Unlimited’

(a) A boundless reservoir from which all things come and to which all things return

(1) This is the first mention of the ‘Law of Return of all Things’ which is still central to the cyclical concepts of astrology

4) Made the first known map of the Earth

5) Second leader of the Milesian School

(a) pupils included Anaximenes and Pythagoras

C) Anaximenes (585-528 BCE)

1) Regarded as an important figure in the development of astronomy, although little is known of his work

2) Developed the notion of ‘macrocosm and microcosm’

(a) ‘As above, so below.’

3) Observed obliquity of the ecliptic

4) Believed stars were like nails attached to transparent spheres of crystalline material which turned around the Earth like a hat on a head

(a) The belief in crystalline spheres persisted, like many other ancient notions up to the work of Johannes Kepler in the 17th century

D) Heraclitus (535-475 BCE)

1) "Weeping Philosopher" & "The Obscure"

2) Believed that change is central to the Universe

(a) "Everything flows, nothing stands still."

(b) "No man can cross the same river twice, because neither the man nor the river are the same."

E) Pythagoras (586-490 BCE)

1) Regarded as one of the most brilliant and influential philosophers of all time

2) Educated in the mathematics of the Ionian school

3) Knew both Thales and Anaximander

4) Studied in Egypt

5) Studied in Babylon

6) Discovered musical notes can be applied to mathematics as he passed a blacksmith shop

(a) The anvils used where all sized in proportion to each other and hence the sound emanating from the striking of

the anvil was based on this proportional size

7) Main theory

(a) Planets in motion moved based on mathematical equations, hence they would create a noise which could be described as a musical note

(b) Used by Kepler

F) Plato (428-347 BCE)

1) The reality we see is only a distorted shadow of the perfect ideal form

(a) Allegory of the Cave

(b) Car accident

2) The most perfect form is the circle

G) Aristotle (384-322 BCE)

1) Two reasons for Earth being round

(a) Ship on the horizon

(b) Earth’s shadow on moon was curved

(1) Flat Earth could not produce a curved shadow

2) Geo-centric model of Solar System

3) Teacher of Alexander the Great

H) Aristarchus (310-230 BCE)

1) Proposed the Earth orbited the sun

2) First to propose the theory that the Earth rotated on an axis

I) Eratosthenes (276-195 BCE)

1) Devised a method for determining the Earth’s circumference to within 5% of the currently accepted value

(a) Eratosthenes knew that on the summer solstice at noon in the city of Swenet (Syene, now Aswan) on the

Tropic of Cancer, the sun would appear at the zenith (directly overhead.) He also knew, from measurement,

that in his hometown of Alexandria, the angle of elevation of the Sun would be 1/50 of a full circle (7°12')

south of the zenith at the same time. Assuming that Alexandria was due north of Syene he concluded that the

distance from Alexandria to Syene must be 1/50 of the total circumference of the Earth. His estimated distance

between the cities was 5000 stadia (about 500 miles or 950 km.) He rounded the result to a final value of 700

stadia per degree, which gives a circumference of 252,000 stadia. While it is not known the exact size of the

stadion he used, if we assume that Eratosthenes used the "Egyptian Stadium" of about 157.5 m, his

measurement turns out to be 39,690 km (the actual value is 40,075.16 km or 24,901.55 miles). His error is

less than 5%!

J) Hipparchus (190-120 BCE)

1) Regarded as the greatest and most influential astronomer of the ancient world (and the only ancient astronomer

featured on the Astronomer's Monument at Griffith Observatory in Los Angeles, CA)

2) Discovered precession

(a) The Earth's axis rotates (precesses) similar to a spinning top

(b) Period of precession is about 26,000 years

3) North Celestial Pole will not always point towards the same starfield

(a) Polaris today

(b) 3000 BCE - Thuban, a star in the constellation of Draco

4) Catalogue of stellar magnitudes

K) Ptolemy (90 BCE-168 CE)

1) Ensured the continuation of Aristotle’s geocentric model by fitting it to a mathematical model

2) Explained how planets appear to move faster, move slower, and appear to stop and go backward over a period of time

(a) Retrograde motion

(1) Motion accounted for by placing planets on small circles (epicycles) which moved along larger circles (deferents)

3) Work published in the Almegest - 140 CE

Aristotle

Aristotle, more than any other thinker, determined the orientation and the content of Western intellectual history. He was the author of a philosophical and scientific system that through the centuries became the foundational support for both medieval Christian and Islamic scholastic thought. Until the end of the 17th century, Western culture was Aristotelian. Even after the intellectual revolutions of centuries to follow, and of our present intellectual knowledge, Aristotelian concepts and ideas remain an important and integral part of Western thinking.

Aristarchus

The only surviving work of Aristarchus, On the Sizes and Distances of the Sun and Moon, is not based on his sun-centered theory, which unfortunately has been lost. However, his surviving work provides the details of his remarkable geometric argument, based on observation, whereby he determined that the Sun was about 20 times as distant from the Earth as the Moon, and 20 times the Moon's size. Both these estimates were an order of magnitude too small, but the fault was in Aristarchus's lack of accurate instruments rather than in his correct method of reasoning.

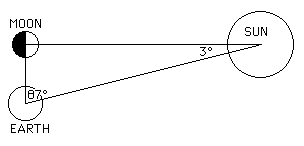
The diagram shows an argument used by Aristarchus. He knew that the moon shines by reflected sunlight, so he argued, if one measured the angle between the moon and sun when the moon is exactly half illuminated then one could compute the ratio of their distances.

Aristarchus estimated that the angle at the time of half illumination was 87 so the ratio of the distances is sin 3. Of course, this is done now using modern notation. Aristarchus did not use degrees nor had trigonometry been invented so he did not have the sine function at his disposal. However, this is in effect the calculation he made, correct in principle yet almost impossibly difficult to observe in practice since determining the moment at which half illumination of the moon occurs can only be very inaccurately determined.

Aristarchus was then faced with calculating an approximation for what is sin 3. He obtained the inequality

1/18 > sin 3 > 1/20

and deduced that the sun was between 18 to 20 times as far away as the moon. In fact at the moment of half illumination the angle between the moon and the sun is actually 89 50' and the sun is actually about 400 times further away than the moon.

Eratosthenes

Despite being a leading scholar, Eratosthenes was considered to fall short of the highest rank. While he was recognized by his contemporaries as a man of great distinction in all branches of knowledge, in each subject he just fell short of the highest place of honour. This distinction gave him the nickname "Beta" or "Pentathlos" both of which refer to as "being second." Today, we know this is a harsh nickname to give to a man whose accomplishments in many different areas are remembered today not only as historically important, but, remarkably still providing a basis for modern scientific methods.

Thales

Thales believed the principle of all things is water, which should not be considered exclusively in a materialistic and empirical sense. It was to be considered that which has neither beginning nor end and as an active, living, divine force. Thales was induced to this belief by the observation that all living things are sustained by moisture and perish without it.
Anaximander

Anaximander said the first animals were fish, which sprang from the original humidity of the earth. Fish came to shore, lost their scales, assumed another form and thus gave origin to the various species of animals. Man thus traces his origin from the animals. Because of this, Anaximander has come to be considered the first evolutionist philosopher.
Anamimenes

For Anaximenes, the first principle from which everything is generated is air. Air, through the two opposite processes of condensation and rarefaction (which are due to heat and cold), has generated fire, wind, clouds, water, heaven and earth. Thus like Thales and Anaximander, he has reduced the multiplicity of nature to a single principle, animated (hylozoism) and divine, which is the reason for all empirical reasoning.
Heraclitus
Heraclitus disagreed with Thales, Anaximander, and Pythagoras about the nature of the ultimate substance and claimed instead that everything is derived from the Greek classical element fire, rather than from air, water, or earth. This led to the belief that change is real, and stability illusory.
Pythagoras

Pythagoras is most remembered for his famous geometry theorem. However, it was not Pythagoras that developed the theorem. The theorem was known to the Babylonians 1000 years before Pythagoras was born. Pythagoras was the first to prove the theorem correct.

Plato's Academy

The best overview of Plato's views can be gained from examining what he thought a proper course of education should consist:

"...the exact sciences - arithmetic, plane and solid geometry, astronomy and harmonics would be studied for 10 years. Then dialectic, which is the art of conversation and answer; the ability to pose and answer questions about the essences of things..."

Plato's Academy flourished until 529 CE when it was closed down by the Christian Emperor Justinian who claimed it was a pagan establishment. Having survived for 900 years it is the longest surviving university known. The sign over his school stated:

"Let no one unversed in geometry enter here."

Hipparchus

The main contributions of Hipparchus includes the production of a table of chords, an early example of a trigonometric table. Some historians have put forth the idea that trigonometry was invented by him. The purpose of this table of chords was to give a method for solving triangles which avoided solving each triangle from first principles. Hipparchus also introduced the division of a circle into 360 degrees.

Hipparchus calculated the length of the year to within 6.5 minutes and discovered the precession of the equinoxes. Hipparchus's value of 46" for the annual precession is good compared with the modern value of 50.26" and much better than the figure of 36" that Ptolemy was to obtain nearly 300 years later. It is believed that Hipparchus's star catalogue contained about 850 stars, not listed in a systematic coordinate system but using different ways to designate the position of a star. His star catalogue, completed around 129 BCE, has been claimed to have been used by Ptolemy as the basis of his own star catalogue.

Ptolemy

One of the most influential Greek astronomers and geographers of his time, Ptolemy propounded the geocentric theory into a form that prevailed for 1400 years.

The Almagest is the earliest of Ptolemy's works and gives in detail the mathematical theory of the motions of the Sun, Moon, and planets. Ptolemy made his most original contribution by presenting details for the motions of each of the planets. The Almagest was not superseded until Copernicus presented his heliocentric theory in the book De Revolutionibus of 1543.

The final five books of the Almagest discuss planetary theory. This is Ptolemy's greatest achievement since there does not appear to have been any satisfactory theoretical model to explain the complicated motions of the five planets before the Almagest. Ptolemy combined the epicycle and eccentric methods to give his model for the motions of the planets. The path of a planet "P" consisted of circular motion on an epicycle, the center "C" of the epicycle moving round a circle whose center was offset from the earth. The planetary theory which Ptolemy developed here is a sophisticated mathematical model to fit observational data. The model he produced, although complicated, represents the motions of the planets fairly well.

Troubling observations of varying planetary brightness and retrograde motion could not be accommodated by the firmly held belief that planetary spheres moved with constant angular velocity, and the objects attached to them were always the same distance from the earth because they moved on spheres with the earth at the center.

The "solution" to these problems came in the form concentric spheres: planets were attached, not to the concentric spheres themselves, but to circles attached to the concentric spheres. These circles were called "epicycles", and the concentric spheres to which they were attached were termed the "deferents".

The centers of the epicycles executed uniform circular motion as they went around the deferent at uniform angular velocity and at the same time the epicycles (to which the planets were attached) executed their own uniform circular motion.

However, in practice, even this was not enough to account for the detailed motion of the planets on the celestial sphere. In more sophisticated epicycle models further "refinements" were introduced that put epicycles on epicycles.

The fact that ancient astronomers could convince themselves that the elaborate scheme of epicycles could still correspond to "uniform circular motion" is testament to the power of three ideas that we now know to be completely wrong. These ideas were so ingrained in the astronomers of an earlier age that they were essentially never questioned. The ideas were:

1. All motion in the heavens is uniform circular motion.

2. The objects in the heavens are made from perfect material and hence cannot change their intrinsic properties.

3. The Earth is at the center of the universe.

These ideas concerning uniform circular motion and epicycles were catalogued by Ptolemy in 150 CE. This picture of the structure of the Solar System has come to be called the "Ptolemaic Universe."

By the Middle Ages, these ideas took on a new power as the philosophy of Aristotle (newly rediscovered in Europe) was adopted to Medieval theology in the great synthesis of Christianity and Reason undertaken by philosopher-theologians such as Thomas Aquinas. The "Prime Mover" of Aristotle's universe became the God of Christian theology, the outermost sphere of the Prime Mover became identified with the Christian Heaven, and the position of the Earth at the center of it all was understood in terms of the concern that the Christian God had for the affairs of mankind.

Thus, the ideas largely originating with pagan Greek philosophers were recognized by the Catholic church and eventually assumed the power of religious dogma. As we will see in our discussion of modern astronomers, to challenge this view of the Universe was not merely a scientific issue. It became a theological one as well and subjected dissenters to the considerable and not always benevolent power of the Church.

< Astronomy of Greece >